随机变量序列的极限的定义

我们知道数列$x_n$的极限定义为:

若对给定的$\delta \gt 0$,我们总能找到一整数$n_0$使得$|x_n-x|\lt \delta$ 对每个$n\gt n_0$都成立.则称$x$为数列$x_n$的极限

但是对于随机变量序列呢? 如果按上面的定义,我们称之为处处($e$)收敛.

无疑,这个要求对于随机变量来说太苛刻了:它要求在$n_0$次试验的结果大致相同.这对随机事件大都不太可能. 所以,我们要在较弱的意义下规定随机变量序列的极限:

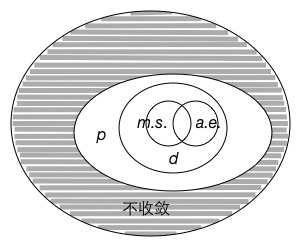
几乎处处收敛,以概率1收敛($a.e.$): 如果对于$n \to \infty$,有$\lim X_n(\zeta)=X(\zeta)$中事件$\zeta$的概率等于1.记为 $$ P\lbrace X_n \to X\rbrace =1, n \to \infty $$
均方收敛($m.s.$): $$ E\lbrace |X_n-X|^2\rbrace \to 0, n\to \infty $$
依概率收敛($p$): $$ P\lbrace |X_n-X| \gt \delta\rbrace \to 0, n\to \infty $$
依分布收敛($d$): $$ F_n(x)\to F(x), n\to\infty $$
柯西准则: $$ |X_n-X_{n+m}|\to 0, n\to \infty, m\gt 0 $$

原来数列中的一种极限到随机变量这就变成了这么多极限= =.有兴趣的请查看各种极限的关系.

大数定理

放开随机变量序列极限的概念,我们来看统计学中的一个问题.

在统计学中有这样的说法: 样本数量越多,则其平均值就越趋近于期望值,说明随机中隐含着必然,从物理角度就是随机的微观世界形成了必然的宏观世界.怎么解释的呢?

统计学解释

我们先看看统计学中的解释:

由统计学中的车贝晓夫不等式$P\lbrace |X-\bar X|\lt \delta\rbrace\ge 1-\frac{\sigma^2}{\delta^2}$,如果标准差$\sigma \ll \delta$,事件$\lbrace |X-\bar X|\lt \delta\rbrace$的概率接近于1,故在进行实验时,它将高度必然地出现.

但是对于$\sigma$不太小的时候呢?统计学家也能想出办法:用$\mathfrak E$表示随机变量$X$,若将其重复$n$次,就会产生一个新的实验$\overline{\mathfrak{E}}$,它的随机变量是实验$\mathfrak E$的样本平均$Y=\bar X$,再重复实验$\overline{\mathfrak{E}}$,则有 $$ P\lbrace |Y-\bar{Y}|\lt \delta\rbrace\ge 1-\frac{\sigma^2}{n\delta^2} $$

所以统计学家说,若进行一次实验$\overline{\mathfrak{E}}$,则我们所观察到的样本平均"实际必然地"以不超过误差地等于期望值

但是,统计学家只能说"实际必然/高度必然",但是不能作为任何绝对性的论述.

好了,现在轮上概率论上场了.这里我们不加证明地列出这些大数定理.

伯努利解释:

在伯努利试验中,事件$\mathscr A$的概率等于$p$,并重复实验$n$次,则对任何$\delta\gt 0$, 有 $$ \lim_{n\to \infty}P\lbrace|\frac{k}{n}-p|\le\delta\rbrace=1 $$

强大数定律(波莱尔):

样本平均值不仅依概率而且也概率为1地趋于期望值.

车贝晓夫解释:

若随机变量序列$X_n$不相关,有$\mathbb E\lbrace X_i \rbrace=\eta_i$,$\sigma_{X_i}^2=\sigma_i^2$以及$\frac{\sum_i \sigma_i^2}{n^2}\rightarrow 0$,则在$m.s.$意义下 $$ \overline{X_n}\to \lim_{n\to\infty}\frac{1}{n}\sum_{i=1}\eta_i $$

马尔可夫解释:

辛钦解释:

以上大数定理主要表现为两种形式:弱大数定理和强大数定理.

这样,概率论就给统计学如何得出事件的概率提供了理论依据.

文章目录

概率论10-收敛及大数定理