这一节我们讨论条件的概念

问题

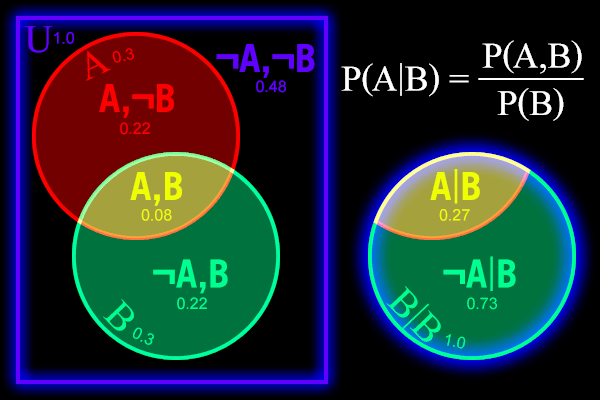
我们都清楚,已知一个具有非零概率的事件$\mathscr M$,在$\mathscr M$下事件$\mathscr A$发生的概率为:

$$P(\mathscr A|\mathscr M)=\frac{P(\mathscr A \mathscr M)}{P(\mathscr M)}$$

如果我们解释成$\mathscr A$在条件$\mathscr M$下的概率等于它们同时发生的概率除以条件$\mathscr M$单独发生的概率, 这种解释就容易混淆: 事件发生分先后么?

解释

我们最好不要用这种解释,因为它引进了同时的概念,但实际上,同时表示的仅仅是发生的事件$\mathscr A$也刚好意味着发生了事件$\mathscr M$.

在上节中,我们提到事件是结果的集合,这里提供集合论中的解释: 事件$\mathscr A$代表概率空间中的一个集合,$\mathscr M$是另一个集合,而$\mathscr{AM}$指的是$\mathscr{A\cap M}$.而条件概率指的是我们把事件$\mathscr M$中不出现的所有试验结果都丢弃不管,而只保留它出现的的试验结果,在这些试验结果中$\mathscr{A}$出现的概率.

也就是我们把概率空间转换到事件$\mathscr M$中考虑.

Alt
条件概率转换

独立事件

学了条件概率, 大部分书上就要讲独立事件了.诸如它的定义:$P(\mathscr{AB})=P(\mathscr A)P(\mathscr B)$及必要条件$P(\mathscr A|\mathscr B)=P(\mathscr A)$等等,但是,什么是独立事件?

  • 独立事件必然是时间上(重复试验)或空间上(多随机变量)的,它与条件概率没有必然的联系,和互斥事件根本就是不同维度的东西.
  • 互斥事件按之前我们叙述的很好理解,就是在同一个概率空间中两个事件交集为空.

在这里举几个独立事件的例子:

  • 重复扔骰子,第一次的事件和第二次的事件是独立事件.
  • 我一只手扔1号骰子,同时另一只手扔2号骰子,这两个事件是独立事件

贝叶斯定理

作为条件概率的一种最重要定理,其公式为: $$P(\mathscr{A}|\mathscr B)=\mathscr{A}\frac{P(\mathscr B|\mathscr{A}}{\mathscr{B}}$$

即总结为:

后验概率 = 先验概率 * 调整因子

这里有一篇比较好的文章供参考

全划分

我们称$\mathscr{A_1},\ldots,\mathscr{A_n}$是概率空间的一个全划分,如果它们是互斥的且其和为整个概率空间.

全概率公式

如果$\mathscr A, \mathscr B$互斥,则有:

$$P(\mathscr A + \mathscr B|\mathscr M)=P(\mathscr A|\mathscr M)+P(\mathscr B|\mathscr M)$$