概率论4-独立事件

在前一章,我们提到了独立事件,并指出了什么是独立事件,但是还是有些模糊的.独立事件之于概率论,是有其特殊意义的.书上说,由于独立性概念才使得概率论没有仅被当作测试论的一个分支,而发展成一门与之分离的学科. 我们可以看出,独立的概念有独立于概率论的一面. 那么,为什么会有独立事件?

概率论是讨论单个实验的结果及由这些结果构成的事件.但是在应用中,往往要涉及两个或多个实验或同一实验的多次重复.所以我们必须设想一个组合实验,它的结果是多重对象,其概率空间,就集合论来讲,是多个对象的笛卡儿乘积. 如果多重对象间相互关联,这种乘积就没有意义,我们可能要设计很复杂的运算才能实现.但是如果多重对象间没有关联,那么事性就简单了. 这就是独立事件. 在科研中我们经常假设的条件之一.

笛卡儿乘积空间

我们定义两个集合$\Omega_1$和$\Omega_2$的笛卡儿乘积为

$$\Omega=\Omega_1\times \Omega_2$$

它类似于二维直角空间.

类似的,

两实验的概率空间亦为$\Omega=\Omega_1\times \Omega_2$, 此实验可记为 $$\mathfrak{E}=\mathfrak{E_1}\times \mathfrak{E_2}$$

我们同时假定实验1和实验2中的事件是独立的. 注意,这里实验1和实验2可能是不同的实验也可能是同一实验的重复.

空间之和

我们定义两个集合之和为$\Omega=\Omega_1+\Omega_2$为所有那些在集合1和集合2中的元素组成的集合.

概率空间之和: 若$\Omega_1\Omega_2=\emptyset$,则上面的和$\Omega$可看作是又一实验的空间,此实验可记为$\mathfrak E = \mathfrak E_1 + \mathfrak E_2$

我们天然地理解笛卡儿乘积空间,但是对和空间比较陌生.在这里举一个例子:

一箱内有10个白球与5个红球,第二个箱内有20个白球与20个红球,我们随机地选中一箱,再从中取出一球,问取得白球的概率是多少?

这里我们把第一个箱和第二个箱取球视为实验1和实验2,此时和空间由$\Omega=\Omega_1+\Omega_2$构成,且选择概率均等.

伯努利试验

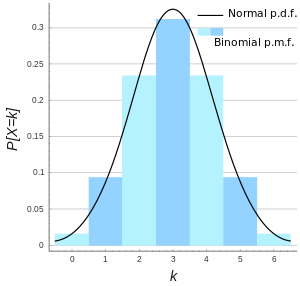
伯努利试验描述了在$n$次独立试验中出现$k$次的概率,可以用二项分布概括.

$$p_n(k)={n \choose k}p^kq^{n-k}$$

其中最可能成功的次数为$k_{\max}=\lfloor (n+1) \rfloor$

渐近定理

当$n$很大时,上面二项分布的概率就比较难计算了.所以有了渐近定理:

当$npq\gg 1$时, $p_n(k)\approx \frac{1}{\sqrt{npq}}G(\frac{k-np}{\sqrt{npq}})$ 其中$G(x)$为高斯函数

称为de Movire-Laplace定理. 该定理是中心极限定理(CLT)的最初版本.它指出大量相互独立的服从二项分布的随机变量,它的极限是正态分布.

近似求$k_1\le k \le k_2$的概率, 可视为对高斯函数求积分:

$$\sum_{k=k_1}^{k_2}{n \choose k}p^kq^{n-k}\approx erf\frac{k_2-np}{\sqrt{npq}}-erf\frac{k_1-np}{\sqrt{npq}}$$

其中$erf()$为误差函数,即高斯函数的积分.

大数定理

由上面的式子我们可以推出: 若$n$足够大,则$k/n$将无限接近于$p$.

这里我们第一次接触到大数定理的含义:样本数量越多或重复次数越多,其平均值就越趋近于期望值.

广义伯努利试验

$$p_n(k_1,k_2,\ldots,k_r)=\frac{n!}{k_1!k_2!\cdots k_r!}p_1^{k_1}p_2^{k_2}\cdots p_r^{k_r}$$